Решение задания № 6

Экономический факультет МГУ. Отделение экономики, 1995 год.

	(1)	Решаем иррациональное уравнение с параметром p. Для этого возводим обе части уравнения (1) в квадрат.
(x - 2)2 = - 2 (p + 2) x + 2	(2)	Раскрываем скобки и приводим подобные слагаемые в уравнении (2).
x2 - 4 x + 4 = - 2 (p + 2) x + 2	(3)	Переносим все слагаемые в одну часть и получаем квадратное уравнение для x.
x2 + 2p x + 2 = 0	(4)	Решаем квадратное уравнение (4) через дискриминант D/4 = p2 - 2 и находим корни при p2 ³ 2.
	(5)	Теперь следует отсечь побочные корни уравнения (4), приобретенные за счет возведения уравнения (1) в квадрат.
x - 2 ³ 0, или x ³ 2	(6)	Используем дополнительное условие, которому должны удовлетворять решения уравнения (1), вытекающее из неотрицательности арифметического корня в правой части формулы (1).
	(7)	Выясним, при каких значениях параметра p первый корень уравнения (4) является также и корнем уравнения (1).
	(8)	Решаем для этого иррациональное неравенство, относительно параметра  p.
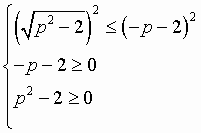	(9)	Стандартный метод решения данного неравенства состоит в возведении обеих частей в квадрат и наложении дополнительных условий на подкоренное выражение и правую часть неравенства (8), которая не может быть отрицательной.
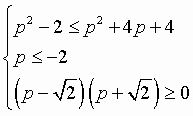	(10)	Раскрываем скобки.
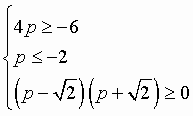	(11)	Приводим пободные слагаемые.
	(12)	Из полученной системы видно, что первые два неравенства не имеют областей пересечения, следовательно, и вся система (12) не имеет решений. Таким образом, при любых значениях параметра p первый корень x1 (7) не удовлетворяет дополнительному условию (6), т.е. является побочным.
	(13)	Теперь выясним, при каких значениях параметра p второй корень уравнения (4) является и решением уравнения (1).
	(14)	Для этого необходимо решить иррациональное неравенство (14), которое, в свою очередь, распадается на две системы неравенств (15) или (16).

Первая система		Вторая система
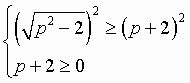	(15)		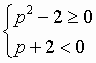(16)
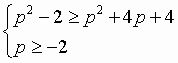	(15.1)		(16.1)
	(15.2)		(16.2)
Решение первой системы (15): pÎ [- 2; - 3/2]	(15.3)	Решение второй системы (16): pÎ (- ¥;- 2)	(16.3)

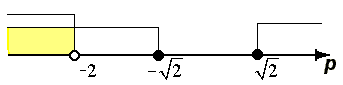Решение иррационального неравенства (14) представляет собой объединение решений систем неравенств (14) и (15), которое можно записать в следующем виде:

Следовательно, второй корень уравнения (4) x₂ (13) удовлетворяет дополнительному условию (6) только в области (17), и только в этой области он является истинным корнем уравнения (1). Таким образом, уравнение (1) имеет единственное решение при значениях параметра: p £ - 3/2.

Web Design: Kurilin A.V. 2003-2007