Решение задания № 1

Экономический факультет МГУ. Отделение экономики, 1995 год.

	(1)	Решаем иррациональное уравнение.
	(2)	Возводим обе части уравнения (1) в квадрат и раскрываем скобки.
x + 3 = 81 - 18x + x2	(3)	Переносим все слагаемые в правую часть формулы (3) и приводим подобные.
81 - 18x + x2 - x - 3 = 0	(4)	Получаем стандартное квадратное уравнение, которое решаем через дискриминант - D.
x2 - 19x + 78 = 0	(5)	D = 192 - 4×78 = 361 - 312 = 49
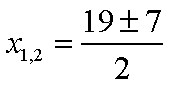	(6)	Находим корни квадратного уравнения (5), среди которых присутствуют и корни уравнения (1).
x1= 13      x2= 6	(7)	Но это еще не ответ!!!

Характерной особенностью всех иррациональных уравнений, которые решаются возведением в квадрат обеих частей, является появление так называемых побочных корней. Дело в том, что уравнение (5) является следствием уравнения (1), но не эквивалентно ему. Среди корней уравнения (5) могут присутствовать и корни другого сопряженного уравнения, отличающегося от уравнения (1) только знаком правой части:

(8)

После возведение в квадрат обеих частей уравнения (8) мы опять цепочку получаем уравнений (2), (3), (4), (5). Следовательно, среди корней уравнения (5) присутствуют как корни уравнения (1), так и корни уравнения (8). Чтобы отличить корни нашего уравнения (1) от корней побочного уравнения (8) можно просто сделать проверку подстановкой найденных решений x₁, x₂ (7) в уравнение (1). Однако этот способ отсечения побочных корней удобен в применении, только в том случае, если получены целые корни. Более эффективен метод дополнительных условий, которые накладываются на искомые решения.

Так как в левой части уравнения (1) стоит арифметический квадратный корень, который может принимать только неотрицательные значения, то и правая часть уравнения (1) должна быть неотрицательной. Это дает нам дополнительное условие, которому должны удовлетворять корни уравнения (1):

Таким образом, уравнение (1) будет эквивалентно уравнению (5), только при наличии дополнительного условия (9). Легко увидеть, что корень   x₁ = 13   не удовлетворяет условию (9), следовательно, он является побочным корнем!

Web Design: Kurilin A.V. 2003-2007