Решение
задания № 5
|
|
Решение
задания № 5
|
|
Экономический факультет
МГУ. Отделение экономики, 1995 год.
|
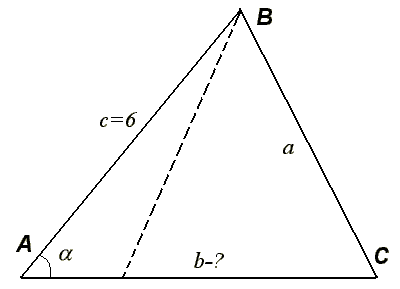
Сделаем рисунок к задаче и введем простые обозначения AB = c, BC = a, AC = b, ÐBAC = a = 30° , радиус описанной окружности обозначим буквой R = 5. Первый шаг в решении задачи связан с использованием теоремы синусов для треугольника ABC и с нахождением стороны BC.
|
 |
Из теоремы синусов вычисляем a = 2R×sina = 5. Теперь воспользуемся теоремой косинусов и выразим сторону ВС через AB и искомую сторону АС.
| a2 = b2+ c2 - 2bc×cosa |
(1)
|
Уравнение (1) можно рассматривать как квадратное уравнение для неизвестной переменной b. Решаем это уравнение через дискриминант.
| b2 - 2bc×cosa + (c2 - a2) = 0 |
(2)
|
| D/4 = c2cos2a - (c2- a2) = a2 - c2sin2a = 25 - 9 = 16 |
(3)
|
 |
(4)
|
Таким образом, задача имеет два решения (см. пунктирную линию на рисунке, указывающую на другое возможное расположение стороны BC).
|
О Т В Е Т:
 |
|
Web
Design: Kurilin A.V. 2003-2007
|
|
|
 |
|
|
|
