Решение задания № 3

Экономический факультет МГУ. Отделение экономики, 1995 год.

	(1)	Для решения указанного неравенства обозначим основание логарифма буквой a и найдем область допустимых значений (ОДЗ) переменной x , входящей в него.
	(2)	Согласно свойствам логарифмической функции y = loga(X) выражение, стоящее под знаком логарифма, а также основание логарифма a должны быть числами положительными. Кроме того, основание логарифма не может быть равно 1. Последнее неравенство системы выполнено для любых значений переменной x, а первые два неравенства сводятся к системе (3).
	(3)	Таким образом, ОДЗ неравенства (1) состоит из множества точек, x > 1/3, или xÎ(1/3; +¥).
		Заметим, что на всей области определения неравенства (1) основание логарифма всегда меньше единицы ( a < 1 ).
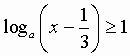
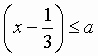	Þ	Поскольку при a < 1 логарифм в левой части неравенства (1) представляет собой убывающую функцию, то при переходе к аргу-ментам логарифмов знак неравенства должен измениться на противоположный. Таким образом, задача свелась к решению простого алгебраического неравенства (4).
	(4)	Переносим все числа в левую часть неравенства (4) и приводим дроби к общему знаменателю. Получаем неравенство (5).
	(5)	Последнее неравенство решаем методом интервалов на числовой оси x (см. рисунок).

Решению неравенства (5) на рисунке соответствуют желтые закрашенные области:
xÎ(-¥; 1/3)È[1/3; 2/3]. Накладываем на это решение ОДЗ (3) xÎ(1/3; +¥) и находим ответ задачи как пересечение указанных интервалов.

Web Design: Kurilin A.V. 2003-2007