Тригонометрия
|
|
Тригонометрия
|
|
Таблица значений основных тригонометрических функций
Значения аргумента из первой четверти: (0º-90º)
|
x (град) |
0º |
15º |
18º |
22,5º |
30º |
36º |
45º |
54º |
60º |
67,5º |
72º |
75º |
90º |
|
x (рад) |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
sinx |
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
cosx |
1 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
tgx |
0 |
|
|
|
|
|
1 |
|
|
|
|
|
*** |
|
ctgx |
*** |
|
|
|
|
|
1 |
|
|
|
|
|
0 |
Значения аргумента из второй четверти: (90º-180º)
|
x (град) |
90º |
105º |
108º |
112,5º |
120º |
126º |
135º |
144º |
150º |
157,5º |
162º |
165º |
180º |
|
x (рад) |
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
sinx |
1 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
cosx |
0 |
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
tgx |
*** |
|
|
|
|
|
-1 |
|
|
|
|
|
0 |
|
ctgx |
0 |
|
|
|
|
|
-1 |
|
|
|
|
|
*** |
Значения аргумента из третьей четверти: (180º-270º)
|
x (град) |
180º |
195º |
198º |
202,5º |
210º |
216º |
225º |
234º |
240º |
247,5º |
252º |
255º |
270º |
|
x (рад) |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
sinx |
0 |
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
cosx |
-1 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
tgx |
0 |
|
|
|
|
|
1 |
|
|
|
|
|
*** |
|
ctgx |
*** |
|
|
|
|
|
1 |
|
|
|
|
|
0 |
Значения аргумента из четвертой четверти: (270º-360º)
|
x (град) |
270º |
285º |
288º |
292,5º |
300º |
306º |
315º |
324º |
330º |
337,5º |
342º |
345º |
360º |
|
x (рад) |
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
sinx |
-1 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
cosx |
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
tgx |
*** |
|
|
|
|
|
-1 |
|
|
|
|
|
0 |
|
ctgx |
0 |
|
|
|
|
|
-1 |
|
|
|
|
|
*** |
|
При отрицательных
значениях аргумента можно использовать формулы:
|
|
|
cos(-x) = cos(x)
|
sin(-x) = - sin(x)
|
|
tg(-x) = - tg(x)
|
ctg(-x) = - ctg(x)
|
В данных таблицах перечислены почти все положительные значения аргумента x, для которых значения основных тригонометрических функций выражаются точно через радикалы (достаточно компактным образом). Однако это далеко не полный перечень значений аргументов с подобными свойствами. Например, синус и косинус шести градусов также могут быть выражены через радикалы:
 |
 |
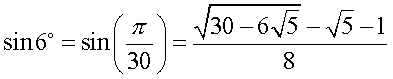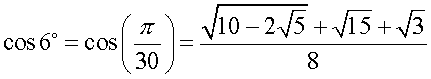Более полная таблица значений тригонометрических функций с 30 углами из первой четверти, изменяющимися с шагом в три градуса, приведена в файле компьютерной программы Maple. , содержащем также решения 9 заданий по математике из "Сборника задач по Математике для поступающих во ВТУЗы" под редакцией М.И.Сканави. Задачи из "СКАНАВИ" посвящены преобразованиям тригонометрических выражений, в которых используются нестандартные углы 18, 36 54 градуса и др. Решения задач получены двумя способами: в аналитическом виде (при помощи формул из школьной тригонометрии) и средствами программы Maple.
Расширенная таблица значений тригонометрических функций
|
Web
Design: Kurilin A.V. 2003-2014
|
|
 |
 |
 |
|
|
|
|
